| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 오블완
- 크래프톤 정글 4기
- 다익스트라
- BFS
- C
- 크래프톤정글4기
- 핀토스
- 이벤트 함수 실행 순서
- kraftonjungle
- 유니티
- c#
- KRAFTON JUNGLE
- 전쟁-전투
- anonymous page
- 백준
- 추상클래스와인터페이스
- 크래프톤정글
- 알고리즘
- User Stack
- 알고리즘수업-너비우선탐색2
- 티스토리챌린지
- 크래프톤 정글
- 연결리스트
- 4기
- 파이썬
- Unity
- 네트워크
- project3
- TiL
- pintos
- Today
- Total
말감로그
그래프 본문
그래프는 비선형자료구조이다. 그러면 비선형자료구조는 무엇인가?
비선형자료구조란?
비선형 자료구조란 데이터를 일렬로 구성하지 않고, 자료 순서나 관계가 복잡한 자료구조이다.
- 자료를 계층적으로 구성한 자료구조, 데이터가 일렬로 연결되는 선형 자료구조와 달리 분기점이나 사이클 등이 존재하여 비선형적인 구조를 가지고 있다.
- 선형 자료구조보다 복잡한 구조를 가지기 때문에 구현 및 관리가 어려울 수 있지만, 적절하게 활용하면 다양한 문제를 해결할 때 도움.
그래프
정점(vertex)이라고 불리는 노드(node)들과 이 정점을 연결해주는 간선(edge)으로 이루어진 자료구조

그래프 관련 용어
- 정점(node,vertex) : 데이터를 저장하는 위치
- 간선(edge, arc) : 정점(노드)를 연결하는 선, 링크 or 브랜치로도 불림.
- edge : 무향 그래프에서 간선을 지칭할 때 사용. 방향성이 없음
- arc : 유향 그래프에서 간선을 지칭할 때 사용. 방향성이 있음 - 인접 정점(adjacent vertex) : 간선에 의해 직접 연결된 정점.
- 경로 : 간선을 따라갈 수 있는 길
- 단순 경로(simple path) : 경로 중에서 반복되는 정점이 없는 경우. (ex.한붓그리기- 같은 간선을 지나가지 않는)
- 차수(degree) : 정점에 연결된 간선의 개수
- 입력 차수(in-degree) : 방향 그래프에서 한 정점으로 들어오는 연결선의 수
- 출력 차수(out-degree) : 방향 그래프에서 한 정점에서 나가는 연결선의 수
- 경로 길이(path-length) : 경로를 구성하는데 사용한 간선의 수
- 사이클(Cycle) : 시작 정점과 종료 정점이 동일한 경우
+한붓 그리기 :그래프 상에서 degree가 홀수인 vertex가 존재하지 않거나 2개인 경우 한붓 그리기를 만족한다고 한다..
그래프 종류
1. 무방향 그래프(Undirected)

두 정점(노드)을 연결하는 간선에 방향이 없는 그래프
노드와 간선으로 이루어져 있으며, 노드 사이의 관계는 양방향.
(A,B)로 표현
2. 방향 그래프(Directed)
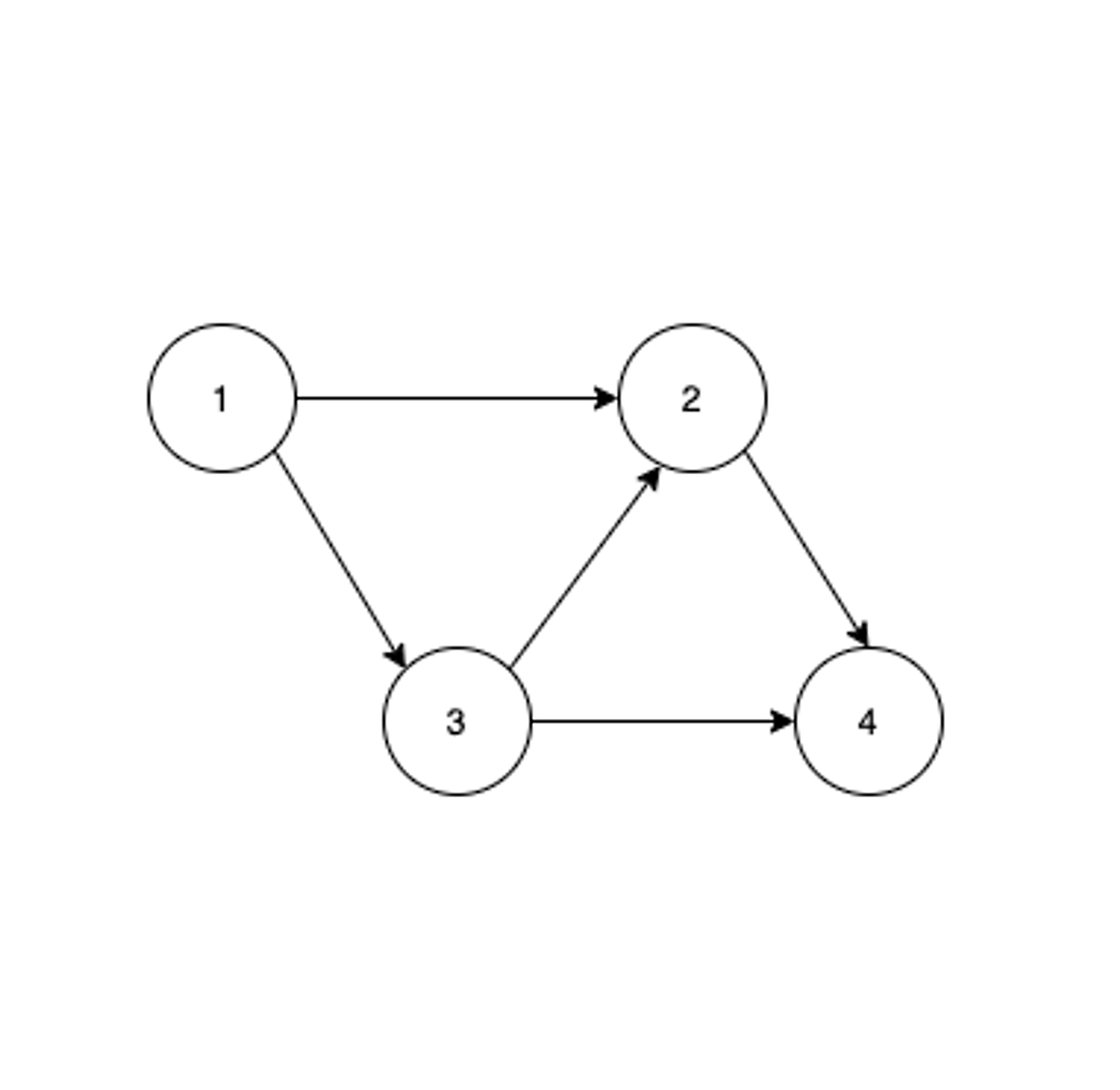
두 정점(노드)을 연결하는 간선에 방향이 존재하는 그래프. 간선이 가리키는 방향으로만 이동할 수 있음.
노드와 간선(아크)으로 이루어져 있으며, 노드 사이의 관계는 일방향
<A,B>로 표현
3. 가중치 그래프(Weighted)
두 정점(노드)을 이동할 때 비용이 드는 그래프
(최단 경로 안내하는 네비게이션, 최저 비용의 경로 탐색)

그래프 표현방식
1. 인접 행렬(Adjacency Matrix)
그래프 간의 관계를 2차원 배열로 표현하는 것이다.
노드 간에 직접 연결되어 있다면 1, 아니면 0을 저장한다.
- 무방향 그래프의 경우 대각선을 기준으로 대칭하게 matrix가 나타나게 되서 이를 절반으로 쪼개도 무난하게 표현할 수 있다.
- 방향 그래프의 경우 한 쪽을 to, 나머지 한 쪽을 from으로 설정하여 matrix에 값을 할당한다.
대신 무방향 그래프의 경우 행과 열의 의미가 서로 동일하지만, 방향 그래프의 경우에는 행과 열의 의미가 서로 다르고 이 각각을 어떻게 설정하느냐에 따라서 matrix에 값이 할당되는 양상도 달라짐을 알아둬야한다.
- 가중치 그래프의 경우 1로 표기했던 부분에 실제 가중치를 입력해주면 된다.

장점
- 구현이 쉽다.
-> 그래프가 어느 정도 작은 경우에는 인접행렬을 더 선호 - 데이터를 탐색하는 시간과 수정하는 시간이 빠르다.
두 정점을 연결하는 간선을 조회할 때 O(1)
정점의 차수를 구할 때 O(n)
단점
- 메모리가 많이 든다.
- 노드에 비해 간선이 적으면 비효율적이게 된다. 예를 들어, 노드가 1억개인데 간선 1개만 갖고 있으면 최악의 경우 1억번 탐색을 해야할 수도 있다.
O(N^2) 시간 소요
2. 인접 리스트(Adjacency List)
그래프 간의 관계를 연결리스트로 표현한 것이다.
노드 번호별로 index를 담아내고, 포인터를 통해 각각을 연결리스트로 묶는 것이다.
각 인덱스의 버킷은 'n번과 연결된 다른 노드들'을 담아두는 것이다.

장점
- 필요한 만큼 공간을 사용하기 때문에 인접 행렬에 비해 상대적으로 공간 낭비가 적다.
- 모든 간선의 수를 알아내려면 각 정점의 헤더 노드부터 모든 인접리스트를 탐색해야 하므로 O(n+e)
단점
- 정점들의 연결 정보를 탐색할 때 O(n)시간 복잡도가 소요된다.
- 구현이 인접 행렬에 비해 어렵다.

'이론 > 자료구조' 카테고리의 다른 글
| DFS,BFS, 다익스트라, 플로이드 와샬 (1) | 2024.02.07 |
|---|---|
| 위상정렬 (0) | 2024.02.07 |
| 복잡도(Big-O ,시간, 공간) (1) | 2024.02.07 |
| Red-BlackTree (0) | 2024.02.03 |
| [C언어] 동적 메모리 할당(Dynamic Memory Allocation) (2) | 2024.02.02 |

